An SR Policy is used to instantiate an ordered list of segments. If your path definition includes several segments, it can be encoded as a list of segment IDs. This SID List will be represented by an SR Policy. With SR Policy, there will not be state information on transit nodes because all path information will be encoded as a SID list (Label Stack in the MPLS data plane and SRH header in the IPv6 Data plane) and pushed into the header.
A dynamic path can be expressed as an optimization objective or a set of constraints (IGP cost, TE Cost, Delay, SRLG etc.) If the head-end has enough information about the topology it computes the SID list according to optimization objective. In this blog I will try to explain “Min-Metric” and “Min-Metric with Margin” optimization objective.
For the Min-Metric optimization objective, I will not give a detailed example because it is already IGP best path, which we are very familiar.
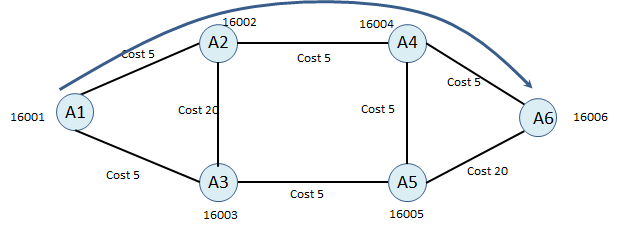
If I have an SR-Policy with Head-end A1, Endpoint A6, Optimization: Min Metric, in that case, my traffic will follow the shortest path. Sid list will only have the Prefix SID of A6.
Incoming Active Segment: NULL Operation: PUSH 16006 Egress Interface: The interface towards to next-hop
This is the expected result.
We have an option optimize min-metric behavior with margin. If you think that, you have different cost for your interfaces but the paths are almost same, or delay of paths are almost identical etc. Shortly if you think that there is no problem with using ECMP even you have the different path costs, you can use margin option.
According to same topology, let’s assume that link between A5 and A6 is very bad link. You never want to use that link if there is other options. But on the other hand, even they have different cost values actual link qualities are slightly different. In that kind of case you use margin option without changing the cost values and you can get the benefit of load sharing.
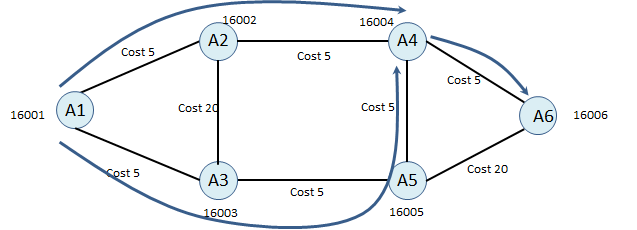
If I have an SR-Policy with Head-end A1, Endpoint A6, Optimization: “Min Metric with margin 6” in that case, when the head-end calculating the SID list, it will add 6 (margin value) to the shortest path cost and it will find a new cost value which will be our maximum cost value. And the head-end will try to share load between the paths which as a lower cost than Maximum cost.
Shortest Path Cost = 15
Maximum Cost = 21 (Shortest Path Cost + Margin)
Path: A1 – A2 – A4 –A6, Cost = 15 (Lower than 21)
Path: A1 – A3 – A5 –A4 – A6, Cost = 20 (Lower than 21)
Traffic will be load shared from A1 to A4 and the final destination will be A6 with the following entries.
Incoming Active Segment: NULL Operation: PUSH 16004 16006 Egress Interface: The interface towards to A2 The interface towards to A3
In this example I assumed our costs are IGP costs. But Min-Metric optimization and Min-metric with margin optimization can be used with also TE Metric and Delay metric.
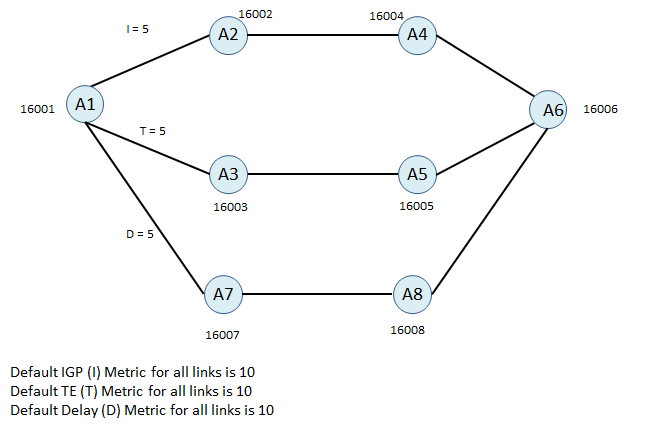
SR Policy 1: Head-end A1, Endpoint A5, Min IGP Metric
Incoming Active Segment: NULL Operation: PUSH 16002 16006 Egress Interface: The interface towards to next-hop
SR Policy 2: Head-end A1, Endpoint A5, Min TE Metric
Incoming Active Segment: NULL Operation: PUSH 16003 16006 Egress Interface: The interface towards to next-hop
SR Policy 3: Head-end A1, Endpoint A5, Min Delay Metric
Incoming Active Segment: NULL Operation: PUSH 16007 16006 Egress Interface: The interface towards to next-hop